Recently I started attending a class at MIT on Statistical Learning Theory and Applications. The course is basically a deep dive into the statistical underpinnings of Machine Learning and I feel it would be very useful for giving me a better understanding of some of the magic going on behind the scenes. I’ve been taking notes throughout and was hoping they might be useful for you all. So let’s get to it!
Lorenzo Rosasco kicks us off with an operationalization of Machine Learning that I haven’t really been exposed to before. This is that the purpose of Machine Learning is to minimize something called “risk”. I’ve usually thought about the minimization of the loss function, but risk (from my understanding) is just an adaptation of the loss function to account for the fact that during training, we can’t calculate the exact value of loss on the hold-out set. The goal, then, is to minimize the expected value of the loss function over all possible X and Y. This is, as I understand it, risk:
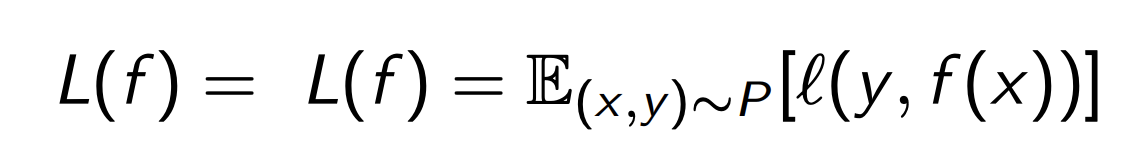
Here is a breakdown of risk vs loss, though they use R instead of L for the risk. Risk breaks down into the integral of the loss function over all values of x and y. That looks like this:
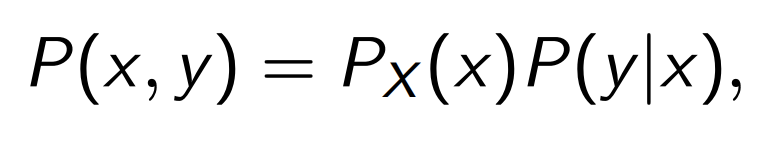
\(\ell\) is the loss, and \(P(x,y)\) is the joint probability. The joint probability accounts for the noise/stochasticity in the learning problem. This joint probability has two components:
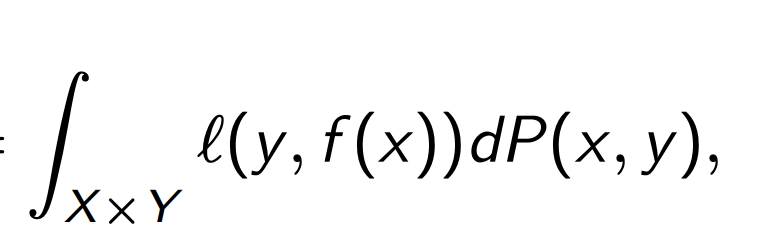
| This is generally true for joint probabilities. In this case, \(P_x(x)\) is the sampling distribution (how X is distributed) and $$ P(y | x) $$ takes into account the relationship between the outcome and the data. The slides have some nice visuals of how differences in these characteristics can really alter how the data look. |
The loss function has been covered better by other people, so I’ll leave that to them. Basically, it’s the cost of using the learning function’s output rather than the actual output.
So how do we choose the right learning function? This is essentially the “learning process” in machien learning; pick a set of functions of a certain class (e.g. a linear regression \(y = mx + b\)) and use some algorithm to explore the space of that class of functions to find the function that minimizes the expected risk. For example, in OLS regression we’re finding the weight values that minimize the sum of the squared difference between the predicted value and the actual value.
The pieces I struggle with are going from loss functions to risk and from risk to expected risk. Maybe I’ll investigate these further in a future blog post. But for now, my intuition is that minimization of the expected risk is our target because we:
- Really want to see our model perform well on unseen data
- Never really get to see all X or Y, so we never can really calculate “true” risk
If my understanding is way off, definitely reach out! Or, reach out anyway if you’re interested in chatting more.
More to come!
 Ben
Ben